➗ nauka podstaw matematyki - Nauczanie początkowe
Nauka podstaw matematyki. Uczniowie rozwijają umiejętności logicznego myślenia, ucząc się rozwiązywać zadania i dostrzegać zależności między liczbami. To czas, gdy odkrywają, jak matematyka pomaga im w codziennym życiu – od liczenia pojęć po rozumienie wzorów i schematów otaczającego świata.
Pierwsze kroki w świecie liczb i logicznego myślenia
Nauka Podstaw Matematyki
Matematyka w edukacji wczesnoszkolnej to fundament, na którym dzieci stopniowo rozwijają swoje umiejętności liczenia, rozwiązywania problemów oraz lepszego rozumienia przestrzeni wokół siebie. Już od pierwszych lat nauki poznają podstawowe działania matematyczne, takie jak dodawanie i odejmowanie, a następnie stopniowo opanowują tabliczkę mnożenia oraz dzielenie. W tym samym czasie uczą się rozpoznawać kształty geometryczne, co pomaga im w lepszym zrozumieniu otaczającego świata. Nauka podstaw matematyki nie jest jedynie serią schematycznych ćwiczeń, lecz procesem, który wpływa na rozwój logicznego myślenia i zdolności analitycznych.
Stosowanie nowoczesnych technik dydaktycznych, takich jak gry edukacyjne, zabawy ruchowe oraz angażujące ćwiczenia praktyczne, sprawia, że dzieci chętniej się uczą i lepiej zapamiętują nowe informacje. Połączenie teorii z praktyką jest kluczowe – dzięki temu dzieci łatwiej przyswajają abstrakcyjne pojęcia i stosują zdobytą wiedzę w codziennych sytuacjach. Matematyka w edukacji wczesnoszkolnej nie musi być trudna ani monotonna, jeśli zostanie przedstawiona w sposób przystępny i interesujący. Nauczyciele oraz rodzice mogą wspierać uczniów, stosując interaktywne ćwiczenia, kolorowe materiały edukacyjne czy nawet zabawy wykorzystujące przedmioty codziennego użytku.
PAMIĘTAJ, ŻE…
Nie chodzi tu wyłącznie o naukę liczenia, ale także o stopniowe budowanie pewności siebie w rozwiązywaniu zadań matematycznych. Wspieranie dzieci poprzez pozytywne podejście, cierpliwość oraz docenianie ich wysiłku sprawia, że nabierają one większej motywacji do nauki. Im częściej mają możliwość praktycznego zastosowania swoich umiejętności, tym lepiej radzą sobie z trudniejszymi zagadnieniami w przyszłości. Dlatego tak ważne jest, aby matematyka w edukacji wczesnoszkolnej była przedstawiana w atrakcyjny sposób, dostosowany do potrzeb i możliwości najmłodszych uczniów.
ułamki dla dzieci klasa 1-3
 Ułamki czyli części całości
Ułamki czyli części całości
Całością może być wszystko: cała czekolada, cała kartka papieru, czy całe jabłko. Ważne jest, żeby kawałki, na które dzielimy całość, były równe.
- Pojęcie: Każda z tych części to połowa.
- Przykład: Jeśli masz litr soku i podzielisz go na dwie równe porcje, każda porcja to będzie pół litra.
- Pojęcie: Każdy z tych małych, równych kawałków to czwarta część lub ćwierć.
- Przykład: Jeśli podzielisz całą czekoladę na cztery równe kawałki, każdy kawałek to ćwierć czekolady.
- Tak jak w przypadku połowy, w życiu spotykamy się z tym, odmierza się płyny (np. ćwierć litra soku).
Pamiętaj: Musimy mieć cztery równe części, żeby złożyć z nich całą całość.
- Przykład: Wyobraź sobie, że masz okrągłą pizzę podzieloną na cztery równe kawałki. Zjadłeś trzy z nich.
| Dzielimy całość na: | Nazwa każdego kawałka: |
|---|---|
| Dwie równe części | Połowa (1/2) |
| Cztery równe części | Czwarta część lub Ćwierć (1/4) |
Uczeń musi rozumieć i używać pojęć: połowa, dwie równe części, cztery równe części, czwarta część lub ćwierć. Ta umiejętność jest wykorzystywana do dzielenia przedmiotów, takich jak kartka papieru czy czekolada.
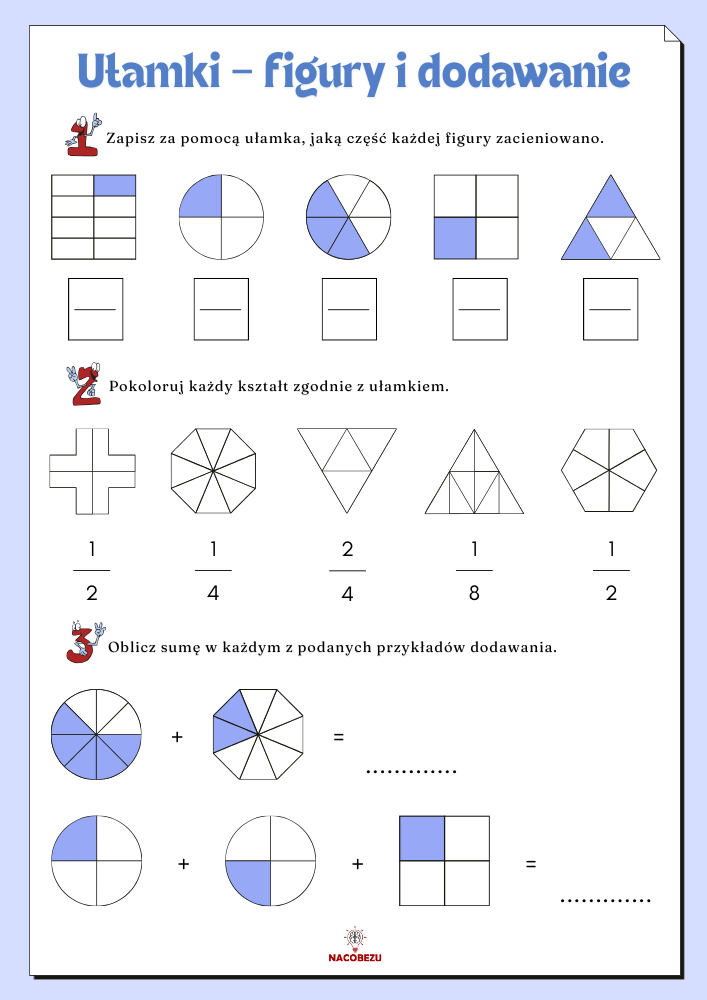
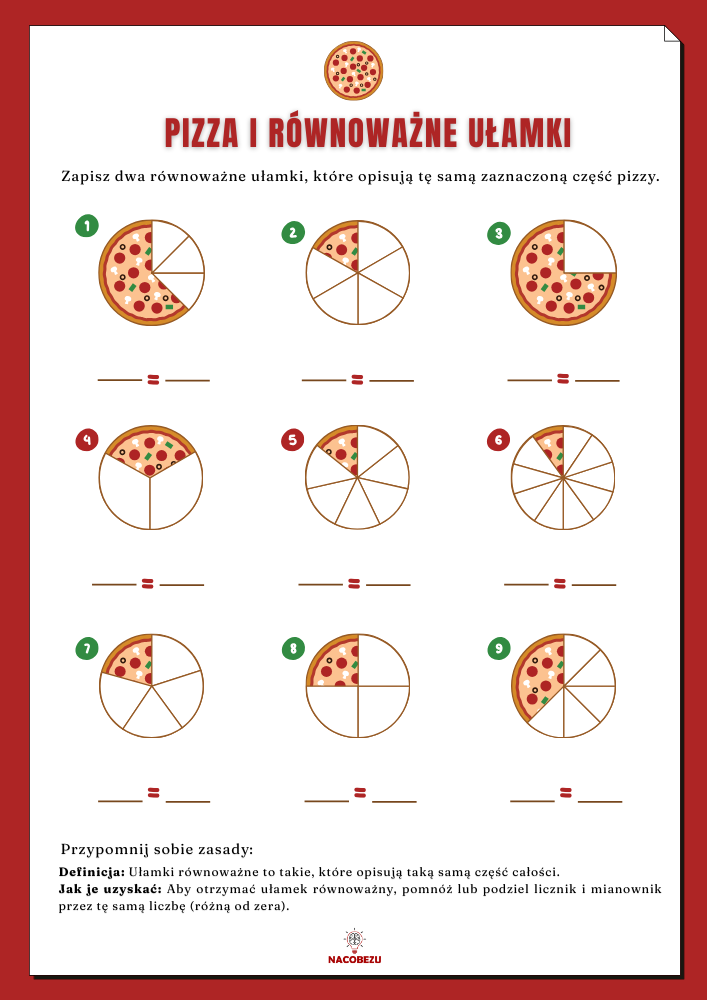
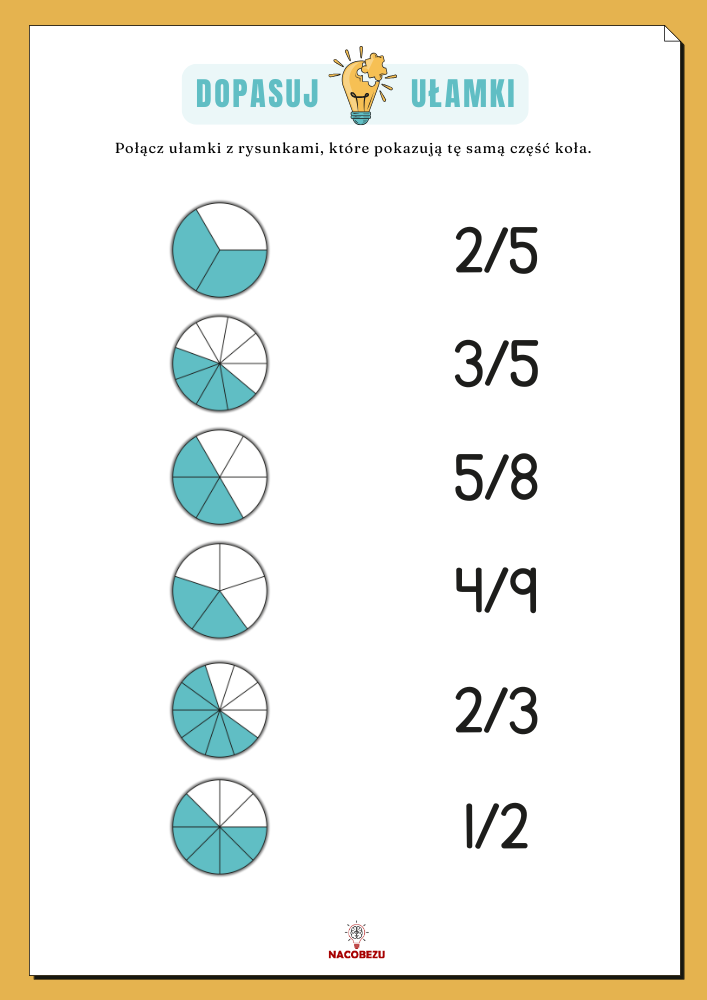
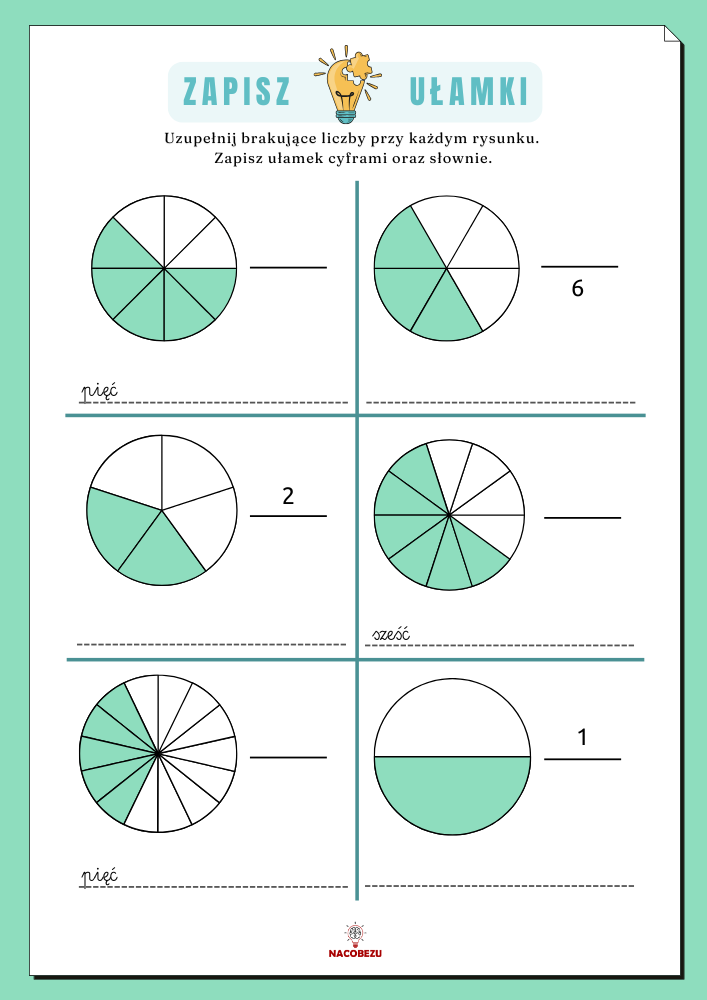
ułamki dla dzieci klasa 1-3 – kaRTY EDUKACYJNE
POBIERZ 📥 – WYDRUKUJ 🖨️ – UZUPEŁNIJ ✏️
ułamki dla dzieci klasa 1-3 – Infografika matematyczna
Ułamki, czyli części całości
Kolorowa infografika „Ułamki jako część całości” pokazuje dzieciom na prostych przykładach, czym jest połowa, jedna czwarta i trzy czwarte. Pizza, jabłko i tabliczka czekolady pomagają zrozumieć, że ułamek to po prostu kilka równych części całej rzeczy – np. 1 z 2 kawałków pizzy, 1 z 4 części jabłka czy 3 z 4 części czekolady. Dzięki obrazkom uczniowie widzą, że liczby w zapisie ułamka mówią, na ile części dzielimy całość i ile z tych części bierzemy.
Zalety infografiki:
Pokazuje ułamki na jedzeniu, które dzieci znają z codziennego życia, więc łatwo łączą matematykę z doświadczeniem.
Uczy krok po kroku: najpierw dzielimy całość na równe części, a potem zaznaczamy, ile z nich bierzemy.
Pomaga zapamiętać podstawowe ułamki (1/2, 1/4, 3/4) i ich nazwy w przyjazny, obrazkowy sposób.
Jak możesz wykorzystać infografikę?
- Możesz wyświetlić infografikę na tablicy interaktywnej lub dużym ekranie i krok po kroku omawiać z dziećmi, jak zmienia się cały przedmiot, gdy zaznaczamy tylko połowę, jedną czwartą lub trzy czwarte.
- Poproś dzieci, aby wymyśliły własne przykłady dzielenia na części, np. podział czasu na zegarze, miejsc w rzędzie krzeseł, kredek w pudełku czy stron w książce, a następnie spróbowały opowiedzieć, jaką część całości stanowi wybrany fragment.
- Możesz także wydrukować infografikę w formacie A4 i wykorzystać ją do pracy w parach lub indywidualnie – jako punkt wyjścia do rysowania własnych „ułamkowych” obrazków.
ułamki dla dzieci klasa 1-3 – pytania do Infografik o ułamkach
możesz je użyć ustnie, w karcie pracy albo jako mini‑quiz
Ułamek jako część całości
- Co oznacza liczba na górze ułamka, a co liczba na dole?
- Jaką część pizzy przedstawia zapis 1/2 i co to znaczy „dwie równe części”?
- Na ile równych części podzielono jabłko, jeśli jedna część to 1/4 całego jabłka?
- Wyjaśnij własnymi słowami, co oznacza ułamek 3/4 tabliczki czekolady.
- Podaj inny przykład z życia codziennego, w którym można użyć ułamka 1/2, 1/4 lub 3/4.
Budowa ułamka i podstawy
- Jak nazywają się części ułamka: liczba na górze i liczba na dole?
- Co informuje licznik, a co mianownik w ułamku 1/2 pokazanym na pizzy?
- Dlaczego mówimy, że ułamek jest „częścią całości”? Podaj przykład.
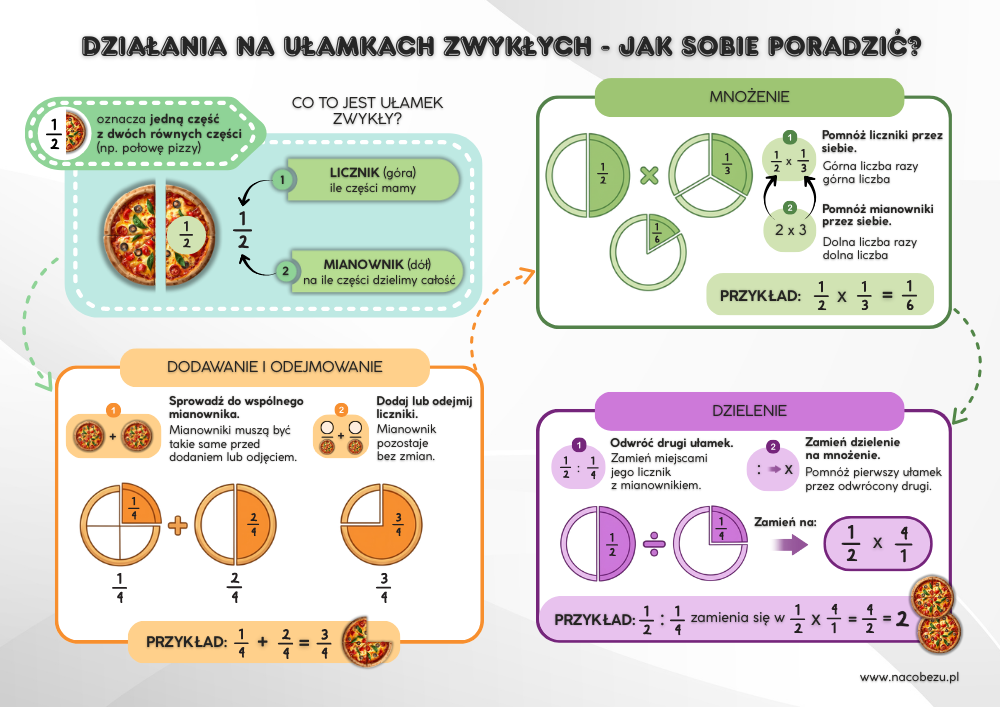
Dodawanie i odejmowanie ułamków
- Co trzeba zrobić najpierw, zanim dodamy lub odejmiemy dwa ułamki o różnych mianownikach?
- W ułamkach o tym samym mianowniku: które liczby dodajemy lub odejmujemy – liczniki czy mianowniki?
- Jaką wspólną nazwę ma liczba zapisana pod kreską ułamkową w obu składnikach działania?
- Co oznacza, że „sprowadzamy ułamki do wspólnego mianownika”? Wyjaśnij jednym zdaniem.
Mnożenie ułamków
- Jakie dwie czynności wykonujemy przy mnożeniu dwóch ułamków zwykłych?
- Co powstaje z liczenia „górna liczba razy górna liczba” i „dolna liczba razy dolna liczba”?
- Wytłumacz na przykładzie, dlaczego wynik 1/2 x 1/3 jest mniejszy niż każdy z tych ułamków.
Dzielenie ułamków
- Co robimy z drugim ułamkiem w działaniu, gdy chcemy wykonać dzielenie ułamka przez ułamek?
- Jak nazywa się ułamek, który powstaje po zamianie miejscami licznika i mianownika?
- Jak przekształcić działanie dzielenia ułamków na mnożenie? Opisz w dwóch krokach.
Pytania podsumowujące
- Wymień trzy sytuacje z życia codziennego, w których przydatne są działania na ułamkach.
- Która część infografiki najbardziej pomaga ci zrozumieć ułamki i dlaczego?